Do you ever feel overwhelmed by the sheer number of tasks you must accomplish? Do you need help figuring out how to track your progress? Calculating percentages can be a great way to measure your progress and ensure you stay on track. Knowing how to calculate percentages can be helpful in any situation, from measuring your academic performance to tracking your goals. In this blog post, we’ll discuss how to calculate the percentage. With the right tools and techniques, you’ll be able to measure your success with ease. So let’s get started!
What is a percentage?
A percentage is a fraction or ratio expressed as a number out of 100. The word “percent” literally means “per hundred.” It represents the relationship between two quantities or values in a fraction of 100. Percentages are commonly used in various settings, from everyday life to scientific research, finance, and business. Understanding ratios is essential to everyday life and is necessary for many tasks, from calculating sales tax to figuring out how much you will owe on loan.
Examples of Percentage:
Here are some more percentage examples:
- 5% = 5/100 ( = 1/20 (or) 0.05)
- 75% = 75/100 ( = 3/4 (or) 0.75)
- 33.3% = 33.3/100 ( = 1/3 (or) 0.3333)
- 20% = 20/100 ( = 1/5 (or) 0.2)
- 90% = 90/100 ( = 9/10 (or) 0.9)
- 16.67% = 16.67/100 ( = 1/6 (or) 0.1667)
- 2.5% = 2.5/100 ( = 1/40 (or) 0.025)
- 40% = 40/100 ( = 2/5 (or) 0.4)
- 80% = 80/100 ( = 4/5 (or) 0.8)
- 12% = 12/100 ( = 3/25 (or) 0.12)
These are just a few examples of how percentages can be expressed as fractions or decimals. Understanding these relationships is key to using percentages in real-world calculations.
Why are percentages important?
Percentages are essential because they allow us to express relationships between two quantities or values clearly. Here are some reasons rates are important:
- Ease of Comparison: Percentages provide an easy way to compare values, even if the numbers being compared are vastly different. For example, if you want to compare the performance of two stocks, one that gained 50 points and another that earned 10 points, it is easier to compare them as percentages (50% and 10%) rather than as raw numbers.
- Everyday Life: Understanding percentages is essential for simple tasks such as calculating discounts, tips, and taxes. For example, calculating a 15% tip on a restaurant bill or how much sales tax you must pay on a purchase can save you money and prevent errors.
- Business and Finance: Percentages are used extensively in business and finance for financial analysis, budgeting, and investment decisions. For example, businesses use percentages to calculate profit margins, markups, and return on investment (ROI).
- Scientific Research: Percentages are also crucial in scientific research, where they are used to express the accuracy and reliability of measurements and describe the results of experiments and surveys.
Percentages are fundamental to many areas of life, from personal finance to scientific research. Calculating and understanding percentages is a crucial skill that can help you make informed decisions and avoid costly errors.
What is the formula for calculating the percentage of a number?

If you’ve ever been tasked with calculating the percentage of a number, you know that it can be daunting. Fortunately, there is a simple formula that can help you out.
Percentage = (part/whole) x 100
Where “part” is the value you want to find the percentage of, and “whole” is the total value or the reference value.
For example, let’s say you want to find out what percentage of 1000 is represented by the number 250. To calculate this, you would use the formula:
Percentage = (250/1000) x 100 percentage = 0.25 x 100 percentage = 25%
So, the number 250 represents 25% of 1000.
To find the percentage of any number, you need to divide the part by the whole and then multiply the result by 100 to get the percentage value.
It’s important to note that the decimal form of the percentage should always be used in this formula. For example, if you want to calculate 25 percent of a number, you need to use 0.25 as the decimal form of the percentage.
The basic formula for calculating a percentage.
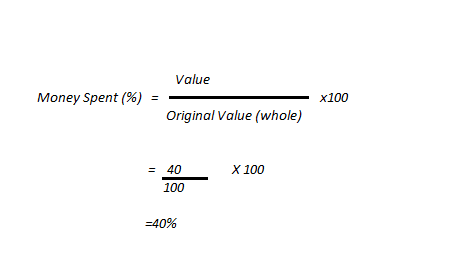
Before diving into more complex calculations, it’s important to understand percentage calculation basics. A percentage is a way of expressing a number as a fraction of 100. For example, 50% means 50 out of 100, or 0.5 decimal.
The percentage formula is as follows: Percentage = (Part/Whole) x 100
To calculate the percentage of a number, divide the part by the whole and multiply by 100. For example, to find out what percentage of 80 is 20, we would use the following formula:
20/80 x 100 = 25%
To calculate the percentage increase or decrease, use the following formula:
Percentage change = ((New value – Old value) / Old value) x 100
For example, if a stock price increased from $100 to $120, the percentage increase would be:
((120 – 100) / 100) x 100 = 20%
To calculate the percentage of a percentage, multiply the two percentages together. For example, if you want to know what percentage of 50% is 10%, you would multiply 50% by 10%:
50% x 10% = 5%
Real-Life Percentage Calculations formula.
Calculating percentages is not just a theoretical exercise; it has many practical applications in daily life. For example, when calculating taxes, tips, and discounts, percentages are often used to determine the final amount.
To calculate the percentage of taxes on a purchase, multiply the pre-tax amount by the tax rate expressed as a decimal. For example, if the tax rate is 7% and the pre-tax amount is $100, the tax amount would be:
$100 x 0.07 = $7
To calculate a tip, multiply the pre-tip amount by the percentage tip rate. For example, if the bill is $50 and the tip rate is 20%, the tip amount would be:
$50 x 0.20 = $10
Calculating the percentage change is also important when analyzing stock prices. For example, if a stock price increased from $50 to $60, the percentage increase would be:
((60 – 50) / 50) x 100 = 20%
Percentage calculations are also crucial in scientific experiments, where the error percentage is used to evaluate experimental results’ accuracy.
Advanced Percentage Calculation formula .
Advanced percentage calculations move beyond the basic percentage formula and more complex calculations. Compound interest is a powerful financial concept that allows money to grow over time. Interest is earned not only on the principal amount but also on any previously earned interest.
The formula for compound interest is:
A = P(1 + r/n)^(nt)
Where: A = final amount, P = principal amount, r = annual interest rate, n = number of times the interest is compounded per year, t = number of years
For example, let’s say you invest $1,000 in a savings account that earns 5% interest compounded annually. After five years, the calculation would be:
A = 1,000(1 + 0.05/1)^(1*5) A = 1,276.28
So after five years, your investment would be worth $1,276.28.
The formula for calculating the percentage difference is:
Percentage Difference = |(New Value – Old Value) / Old Value| x 100
For example, if you had sales of $10,000 in 2020 and $15,000 in 2021, the calculation would be:
Percentage Difference = |(15,000 – 10,000) / 10,000| x 100 Percentage Difference = 50%
So the percentage difference between the two years’ sales is 50%.
The weighted percentage calculation:
To calculate the weighted percentage, multiply each item’s percentage by its weight, then add them together. The formula is:
Weighted Percentage = (%1 x w1) + (%2 x w2) + … + (%n x wn)
For example, let’s say a student’s grades are as follows:
Homework: 90% (weighted 20%) Quizzes: 85% (weighted 30%) Tests: 80% (weighted 50%)
The weighted percentage calculation would be:
Weighted Percentage = (90 x 0.2) + (85 x 0.3) + (80 x 0.5) Weighted Percentage = 83.5%
So the student’s final grade would be 83.5%.
The Percentage Calculations in Business.
Profit margins and markups are two essential concepts in business. Profit margin is the percentage of revenue that is profit, while markup is the percentage of cost that is added to the price to create the selling price.
The formula for profit margin is:
Profit Margin = (Net Profit / Revenue) x 100%
For example, if a company has $100,000 in revenue and $20,000 in net profit, the calculation would be:
Profit Margin = (20,000 / 100,000) x 100% Profit Margin = 20%
So the company’s profit margin is 20%.
The formula for markup is:
Markup = (Selling Price – Cost) / Cost x 100%
For example, if a product costs $50 to produce and is sold for $75, the calculation would be:
Markup = (75 – 50) / 50 x 100% Markup = 50%
So the product has a markup of 50%.
The ROI Formula Is:
ROI = (Net Profit / Total Investment) X 100%
For example, if a company invests $50,000 in a new product line and earns $10,000 in net profit from that investment, the calculation would be:
ROI = (10,000 / 50,000) X 100% ROI = 20%
So the company’s ROI on the latest product line is 20%.
How to convert a percentage to a decimal or fraction

Converting a percentage to a decimal or fraction is an essential daily mathematical operation. Whether you need to calculate a discount on a sale, understand the interest rate on a loan, or convert a percentage to a different format for a math problem, knowing how to convert a percentage to a decimal or fraction is essential. Here’s how to do it:
Converting a percentage to a decimal
To convert a percentage to a decimal, divide the percentage by 100. For example, to convert 25% to a decimal, divide 25 by 100:
25 ÷ 100 = 0.25
So 25% as a decimal is 0.25.
Converting a decimal to a percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent symbol. For example, to convert 0.25 to a percentage, multiply 0.25 by 100 and add the percent symbol:
0.25 x 100 = 25%
So 0.25 as a percentage is 25%.
Converting a percentage to a fraction
To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100 and simplify. For example, to convert 50% to a fraction, write it as:
50/100
Simplify the fraction by dividing both the numerator and denominator by their greatest common factor, which in this case is 50:
50/100 = 1/2
So 50% as a fraction is 1/2.
Converting a fraction to a percentage
To convert a fraction to a percentage, divide the numerator by the denominator, multiply by 100, and add the percent symbol. For example, to convert 3/4 to a percentage, divide 3 by 4, multiply by 100, and add the percent symbol:
3/4 = 0.75
0.75 x 100 = 75%
So 3/4 as a percentage is 75%.
How to add, subtract, multiply, and divide percentages?

Working with percentages in mathematical operations such as addition, subtraction, multiplication, and division is common in everyday life. Here’s how to do it:
Adding and subtracting percentages
To add or subtract percentages, convert them to decimals, then perform the addition or subtraction operation. Afterward, convert the result back to a percentage if needed. For example, suppose you need to add 20% to 50%. Here’s how to do it:
50% + 20% = 0.5 + 0.2 = 0.7
To convert the decimal result back to a percentage, multiply by 100 and add the percent symbol:
0.7 x 100 = 70%
So, 50% + 20% = 70%.
Similarly, to subtract 20% from 50%, follow the same process:
50% – 20% = 0.5 – 0.2 = 0.3
Convert the decimal result back to a percentage:
0.3 x 100 = 30%
So, 50% – 20% = 30%.
Multiplying percentages
To multiply percentages, convert them to decimals, then multiply them as usual. Afterward, convert the result back to a percentage if needed. For example, suppose you need 20% of 50%. Here’s how to do it:
20% of 50% = 0.2 x 0.5 = 0.1
To convert the decimal result back to a percentage, multiply by 100 and add the percent symbol:
0.1 x 100 = 10%
So, 20% of 50% = 10%.
Dividing percentages
To divide percentages, first convert them to decimals, then divide them as usual. Afterward, convert the result back to a percentage if needed. For example, suppose you need to find what percentage 10 is of 50. Here’s how to do it:
10 ÷ 50 = 0.2
To convert the decimal result back to a percentage, multiply by 100 and add the percent symbol:
0.2 x 100 = 20%
So, 10 is 20% of 50.
Common Mistakes to Avoid When Calculating Percentages

Here are some common mistakes to avoid when calculating percentages:
- Forgetting to multiply by 100%: When calculating a percentage, it is essential to remember to multiply the value by 100%. For example, if you want to calculate the percentage of female students in your class, you would divide the number of female students by the total number of students and then multiply the result by 100%.
- Not rounding the answer: When calculating a percentage, it is important to round the answer to the nearest whole number. This is because percentages are often used to make comparisons, and rounding the solution will help to ensure that the comparisons are accurate.
- Making careless errors: When calculating percentages, it is essential to be careful and to avoid making careless errors. This can be done by double-checking your work and by using a calculator.
Not understanding the concept of percentages: It is essential to understand the concept of percentages before calculating them. This will help you to avoid making mistakes and to make better use of percentages.
By avoiding these common mistakes, you can improve your accuracy and efficiency when calculating percentages.
Conclusion:
In conclusion, understanding percentages and being able to calculate them is a critical skill that is necessary for both everyday life and business. Calculating percentages can help calculate taxes, discounts, tips, and even financial analysis in business. Following the steps outlined in this article, anyone can learn how to calculate percentages accurately and avoid common mistakes. Remember always to double-check your work, and convert percentages to decimals before performing mathematical operations. With practice and attention to detail, you can become proficient in calculating percentages and use this skill to make informed decisions in both personal and professional settings.
FAQs - How To Calculate Percentage
What is a percentage?
A percentage is a portion of 100, represented by the symbol “%.” It is a way of expressing a fraction of a whole number, about 100.
Why is understanding percentages important?
Understanding percentages is important because they are used in everyday situations, such as calculating taxes, discounts, and tips. Additionally, percentages are used in financial analysis, such as calculating profit margins and return on investment (ROI).
How do you calculate a percentage?
To calculate a percentage, divide the part by the whole and multiply the result by 100. This gives you the percentage as a decimal, which can be converted to a percentage by multiplying by 100 and adding the “%” symbol.
What is the formula for calculating percentage increase or decrease?
The formula for calculating percentage increase or decrease is ((new value – old value) / old value) x 100. If the result is positive, it is a percentage increase; if it is negative, it is a percentage decrease.
What is compound interest?
Compound interest is interest that is calculated on both the principal amount and any accrued interest. This means that the interest earned in each period is added to the principal, and interest is then calculated on the new total amount.
What is a weighted percentage?
The weighted percentage is a way of calculating the percentage of each individual item’s contribution. It considers the relative importance or weight of each item in the total.
How do businesses use percentages for financial analysis?
Businesses use percentages for financial analysis to calculate profit margins, markups, and return on investment (ROI). These calculations help businesses make informed pricing, investments, and profitability decisions.
What are some common mistakes to avoid when calculating percentages?
Common mistakes to avoid when calculating percentages include forgetting to convert percentages to decimals, using the wrong formula, rounding too early, forgetting to account for the original value, using the incorrect base value, and not checking for reasonableness.









